Coauthored by Vibhu Iyer
CSE 490N: Neural Engineering
Dr. Rao & Dr. Johnson
Tuesday, March 15, 2016
Brain Computer Interfaces are highly complex systems which rely on highly

Figure 1 – ECoG Array – Blausen.com staff. “Blausen gallery 2014”. Wikiversity.
accurate and consistent information processing to properly function. Of course, this information processing is inherently dependent on, once again, accurate and consistent information output from sensors. As such, the near-universal consensus thus far has been that invasive sensor arrays, such as ECoG (Electrocorticography), as pictured to the right, or independent neuron recording electrodes, as in the image to the left. The existing reasons for this comparison center on four distinct confounding factors as presented by Dr. Wu, Dr. Nagarajan, and Dr. Chen in their paper, which will subsequently be reviewed, “Bayesian Machine Learning for EEG/MEG Signal Processing”: Nonstationarity, high dimensionality, subject variability (linked in some ways to #1), and low signal-to-noise ratio (SNR). Based on this research and a set of method reviews, we argue that we can overcome this barrier through the use of probabilistic machine learning methods utilizing Gaussian Processes (GPs). Should this be executed properly, EEG (Electroencephalography) and MEG (Magnetoencephalography) can rival implanted sensor arrays for, primarily, accuracy of control of prosthetics.

Figure 2 – Single Neuron Recording Electrode -ParE, Martin, and Robert H. Wurtz. “Monkey Posterior Parietal Cortex Neurons Antidromically Activated from Superior Colliculus”. Journal of Neurophysiology.
In order to understand how Gaussian Processes in Machine Learning are used in BCI’s, it is essential to first understand Gaussian Processes. A Gaussian Process is a statistical distribution which is observed in a continuous domain such as time or space, as in Figure 3 to the right. In a Gaussian Process, every point in some continuous input is related to a randomly distributed variable. Furthermore, every finite collection of those random variables has a multivariate normal distribution, which is a one-dimensional normal distribution in higher dimensions. This is demonstrated by the Probability Density Function in Figure 4. Gaussian processes are functions of real valued variables and are specified by their mean and covariance functions. The journal article “Gaussian Processes in Machine Learning” states that “a Gaussian Process is a collection of random variables, any finite number of which have (consistent) joint Gaussian distributions” (Rasmussen). This is based on the generalization that the Gaussian Distribution is over vectors and the GP is over functions, which can be seen in Figure 5. The individual random variables in a vector from a Gaussian distribution are recorded by the position of the vector. In the GP, the input and a
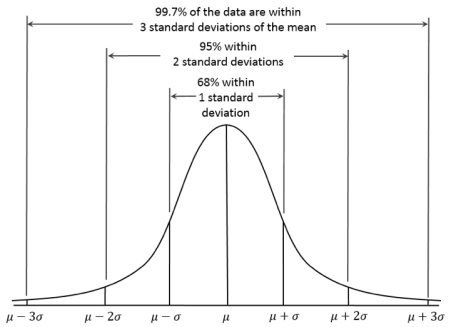
Figure 3 – Normal Gaussian Distribution – JLGentry. “Just an Average Guy”. JLGentry.
dependent variable play the role of the index set. There are multiple GPs, and the Posterior GP is one of them. Posterior GPs are necessary to compute, as they are used to make predictions of unknown test cases. We can let be the known function values and be the function values corresponding to the test set inputs, . This GP is a non-parametric regression technique, where it is necessary to memorize all data points, and use all of these points to predict the data points. The GP inference equation is the unknown data point that is the weighted linear sum of the known data point, and the weights are proportional to its covariance at

Figure 4 – A Multivariate Normal Distribution (Probability Density Function) – Bscan. “Illustration of a multivariate gaussian distribution and its marginals”. Wikimedia.
each known data point. These unknown data points form the basis of machine learning using GPs.
The main goal of Machine Learning (ML) is to build software programs that adapt and learn from experience. The roots of machine learning come from Statistical Pattern Recognition (SPR), Neural Networks and Artificial Intelligence (AI). GPs are a subset of SPR, and are an integral part of ML. “Although working with infinite dimensional objects may seem unwieldy at first, it turns out that the quantities

Figure 5 – “Function values from three functions drawn at random from a GP… The dots are the values generated from [, where applies function to distribution (not GP) values and .] The two other curves have (less correctly) been drawn by connecting sampled points. The function values suggest a smooth underlying function; this is in fact a property of GPs with the squared exponential covariance function. The shaded grey area [represents] the 95% confidence intervals” (Rasmussen) – Rasmussen. University of Cambridge.
for events , , and the corresponding extension to random variables via the sigma algebras generated by them. Marginalization is the operation for abstracting away facts, ‘not wanting to know about’:
” (Seeger). This means that there are subjective beliefs and real observations in Bayesian Theory, and beliefs are updated with real observations. The concept of BML is based off of Thomas Bayes’ idea of AI in which systems are able to learn from past outcomes and predict relationships. This can improve collaboration between humans and machines.
Further Literature Review[1]
Bayesian Machine Learning in a Brain Computer Interface for Disabled Users
Ulrich Hoffman
As shown by Ulrich Hoffman’s work, BML allows for much of human intuition to be automated, which subsequently leads to less error in BCIs. This is defended by his demonstration of reduction of error when paralyzed patients use a BCI to complete a task. Hoffman also demonstrates BML-trained BCIs to be able to solve problems that paralyzed patients would otherwise not be able to solve. In describing the Evidence Framework (EF), the BML derivative algorithm used here, Hoffman states that “an algorithm is obtained that learns classifiers quickly, robustly, and fully automatically. An extension of this algorithm allows to automatically reduce the number of sensors needed for acquisition of brain signals” (Hoffmann). Note that the application of the EF here is to Linear Discriminant Analysis (LDA), a “simple but efficient method for pattern recognition” (Hoffman). The latter portion of the above quote, which discusses a reduction of sensors used, utilizes an algorithm known as Automatic Relevance Determination (ARD). The goal of ARD is to make the analysis of EEG sensor data dynamic based solely on relevant data points. In the context of the discussion points in CSE 490N, this allows the adjustment of the neural regions tracked for Event-Related Desynchronizations (ERDs) and Event-Related Synchronizations (ERSs). Since the tool for Evoked Potential in the subjects was the P300 speller, this primarily served the aforementioned confounding factor of subject variability.
Methods
In this study, subjects were first put through a training process to determine associated neural signals with each of the six images in Figure 6 as they were flashed on a

Figure 6 – Images flashed on laptop screen for subjects – Hoffman, Ulrich. “Figure 6.1”. EPFL.
computer screen. The images were then flashed randomly and, without this data, the Bayesian LDA (BDA) algorithm attempted to discern the order of the images based on EEG signals recorded at 2048 Hz from thirty-two electrodes placed in standard locations. These random image flashes lasted for 100ms each, interspersed with 300ms of random light flashes. The classification model for each of the 4 trials (each lasting approximately thirty minutes) each subject was put through was trained on all previous data. Pre-processing
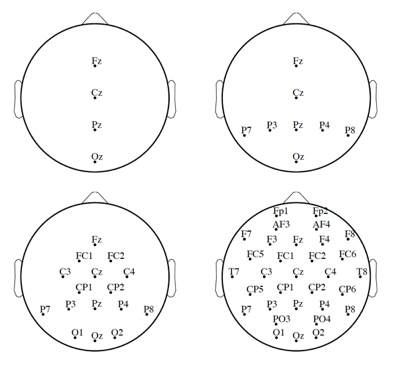
Figure 7 – Different electrode configurations considered – Hoffman, Ulrich. “Figure 6.2”. EPFL.
of all signal data was conducted in the form of referencing to two mastoid electrodes, filtered with a Butterworth bandpass filter, downsampled to 32 Hz, single trial extracted (due to overlap between trials), windsorized (below 10th and above 90th percentiles were standardized to these points due to skew from uncontrollable factors, such as eye blinks, etc.), and scaled. The last two steps of pre-processing directly connect to analysis: first split between four different electrode arrangements (shown in Figure 7), to allow aforementioned optimization based on exclusive electrode consideration, then, of course, the signals were used to form Feature Vectors.
Analysis was run dually using BDA and Fisher’s Discriminant Analysis (FDA), a non-probabilistic ML technique, in order to prove the efficacy of BML. 5 of the subjects were disabled, with different degrees of movement/communication capabilities. The other 4 were able-bodied Ph.D. students.
Results

Figure 8 – CA and Bitrate of 8-electrode arrangement analyzed with BDA. Circles indicate CA and crosses bitrate; S1-S4 are disabled, S6-S9 are able-bodied – Hoffman, Ulrich. “Figure 6.3”. EPFL.
Results were evaluated on Classification Accuracy (ac(B)), which was evaluated by the formula below.
where , where is the classifier output in response to stimulus s, in block b, during run r. B refers to the number of blocks considered. Similarly, R refers to the number of runs.

Figure 9 – Box Plots of Per Block Accuracy (PBA), calculated using CA, for each electrode sampling rate and algorithm (for all subjects) – Hoffman, Ulrich. “Figure 6.4”. EPFL.
Considered simultaneously to CA is Bitrate, which is not necessarily relevant to our consideration, particularly considering inaccuracies based on the lack of signal encoding (resulting in loss at CA below 100%). Both factors are graphed in Figure 8. Numerical comparisons between FDA and BDA at all electrode sampling levels are shown in Figure 9.
Discussion
The simplest takeaway directly from the box plot is that, based on this experiment, BDA displays a significant improvement over FDA for accuracy of signal classification based on images. The analysis of this fact posed by Hoffman states that, though previous studies have shown FDA to be fantastically accurate for small feature sets, large feature sets cause significant detriment to its accuracy (as seen by the fact that FDA-16 has a higher PBA than FDA-32). As such, it may be inferred that BDA poses significant advantages for the particular setting in which EEG is proven to be accurate: large feature set (i.e. large number of electrodes). While this does not necessarily attest to increased ease of accurate ERD/ERS with regard to necessary machinery, it certainly does make the argument that, with a large number of EEG electrodes, as with, in parallel, a large number of electrodes on a Utah or ECoG array, effective data can be detected for use in BCIs.
Bayesian Machine Learning for EEG/MEG Signal Processing
Wei Wu, Srikantan Nagarajan, and Zhe Chen

Figure 10 – An example of VB – Wu, Wei. “FIG4”. IEEE.
In this tutorial-style paper published just two months ago, Dr. Wu, Dr. Nagarajan, and Dr. Chen take the reader through a series of implementations of different forms of BML for EEG/MEG processing. Each of these implementations “identify superior spatiotemporal functional connections” (Wu): Variational Bayesian Methods (VB), Sparse Bayesian Learning Methods (SBL; also discussed by Hoffman in a segment of his extended review outside of our scope of research), and Nonparametric Bayesian Models (NB; one implementation which explicitly utilizes GPs). The first, VB, explicitly exploits the aforementioned basis of BML: the matching of Gaussian estimations/Laplace approximations of unknown features to more reliable models, as per Figure 10 (described in the included description).
SBL, also known as compressed sensing, analyzes a set of distinct generated models fit to provided data on the bases of sparsity and goodness-of-fit. This is optimal, in the context of EEG/MEG, for signals with high dimensionality (as discussed with the large number of correlated electrodes in the Hoffman study), small sample size (similarly relevant to Hoffman) and low SNR.
Finally, NB refers to the implementation discussed towards the beginning of this review with infinite dimensional parameter space GPs. That context having already been provided, we need not go into further detail.
Examples and Method Comparison[2]
An exemplary implementation of SBL for Event Related Potential (ERP) learning is
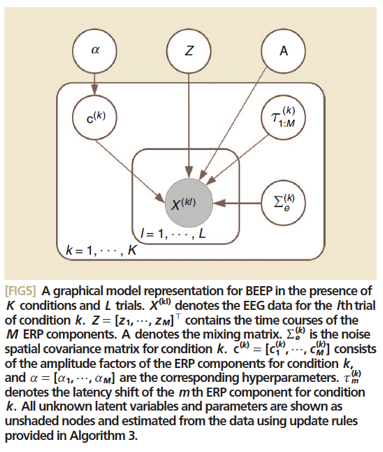
Figure 11 – BEEP Visualization – Wu, Wei. “FIG5”. IEEE.
described by the authors. Initially, a linear representation of said ERPs is developed using each signal component:
where is the EEG signal and is the noise+interference “term from the lth trial of condition k. is the waveform of the mth ERP component, while and are its amplitude factor and latency, respectively. Subsequently generating an inverse Wishart distribution, as per SBL methods, it becomes possible to apply a Bayesian Estimation of ERPs (BEEP) algorithm and generate the most accurate possible algorithm. This is demonstrated visually in Figure 11.
Conclusion
The advantages gained from the application of BML to BCI signal processing does not stop at the efficiency and reliability granted to these devices; as discussed by Hoffman in his paper, there is now possibility for the creation of much more complex BCI technology, ranging from the abstraction of his own demonstrated system to a dialog system, as, perhaps, the generic P300, but grammatically based with BML techniques allowing for near transcription of prescribed thought, to superior online learning. Two particular applications of this are Untrained BCI Use via Expert Models, where models could be pre-trained even before initial users touch the hardware. Thus, it would not be necessary for users to undergo a training period; one would simply start using the device, and it would rapidly adapt. A further abstraction of this would be asynchronicity of BCI use. This is to propose an idle detection of some specific Visual Evoked Potential, perhaps via a Stimulus Display, as in Hoffman’s experiment, for the full activation of the BCI. All in all, the greatest testament of all this is the immense potential that ML as a whole brings to BCIs, particularly in a Bayesian context, and truly of the great things that are yet to come.
Works Cited
BruceBlaus. Intracranial Electrode Grid for Electrocorticography. Digital image. Wikimedia Commons. Wikimedia, 25 Aug. 2014. Web. 15 Mar. 2016.
Hoffmann, Ulrich, Touradj Ebrahimi, and Jean-Marc Vesin. Bayesian Machine Learning Applied in a Brain-computer Interface for Disabled Users. Thesis. Thèse Ecole Polytechnique Fédérale De Lausanne EPFL, No 3924 (2007), Faculté́ Des Sciences Et Techniques De L’ingénieur STI, Programme Doctoral Informatique, Communications Et Information, Institut De Traitement Des Signaux ITS (Laboratoire De Traitement Des Signaux 1 LTS1). Dir.: Touradj Ebrahimi, Jean-Marc Vesin, 2007. Lausanne: Multimedia Signal Processing Laboratory, 2007. Bayesian Machine Learning Applied in a Brain-Computer Interface for Disabled Users. ÉCOLE POLYTECHNIQUE FÉDÉRALE DE LAUSANNE, 3 Sept. 2007. Web. 11 Mar. 2016.
Paré, Martin, and Robert H. Wurtz. Single Neuron Recording/Stimulating Electrode. Digital image. ARTICLES – Journal of Neurophysiology. The American Physiological Society, 1 Dec. 1997. Web. 15 Mar. 2016.
Rasmussen, Carl Edward. “Gaussian Processes in Machine Learning.” Ed. Olivier Bousquet, Ulrike Von Luxburg, and Gunnar Rätsch. Lecture Notes in Computer Science 3176 (2004): 63-71. Cambridge Machine Learning Group Publications. University of Cambridge, 2004. Web. 11 Mar. 2016.
Seeger, Matthias. “Bayesian Modelling in Machine Learning: A Tutorial Review.” Probabilistic Machine Learning and Medical Image Processing (2009): n. pag. Piyush Rai. University of Utah, 21 Mar. 2009. Web. 11 Mar. 2016.
Wu, Wei, Zhe Chen, and Srikantan S. Nagarajan. “Bayesian Machine Learning for EEG/MEG Signal Processing.” IEEE Signal Processing Magazine 33.1 (2016): 14-36. ResearchGate. Web. 11 Mar. 2016.
[1] Note that this is simply an explicit form of the integrated literature review of “Bayesian Modelling in Machine Learning: A Tutorial Review” and “Gaussian Processes for Machine Learning” above.
[2] Entailing, contextually, “results”.